О значении геометрических задач на построение

Решая геометрические задачи на построение, учащимся приходится припоминать все, что он усвоил по геометрии, а именно тот круг сведений, к которому может относиться данная задача.

Например. Если вопрос идет о построении окружности, касающейся трех данных окружностей, то учащейся старается припомнить все, что ему известно об окружности, их касания, пересечения и т.д. и не станет утруждать себя при этом припоминанием формул, выражающих площади поверхности или объема различных геометрических тел.

Таким образом геометрические задачи на построение побуждают учащихся целесообразно припоминать и в этом процессе проявлять логичность рассуждений, так как из припоминаемого необходимо отбирать только то, что дает возможность решить возникший вопрос.

7. Геометрические задачи на построение приучают учащихся проявлять инициативу, изобретательность.

Например: требуется через две данные точки провести окружность, касающейся данной прямой. Учащиеся делают прежде всего соответствующий чертеж, затем принимая во внимание, что KL является касательной к искомой окружности, учащиеся начинают перебирать все, что относится к касательной.

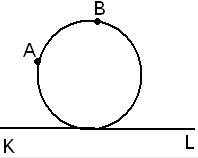
Среди других сведений он вспоминает следующие: если из какой-нибудь точки вне круга, проведем секущую и касательную к нему, то произведение секущей и касательной к нему, то произведение всей секущей на ее внешнюю часть равно квадрату касательной. На чертеже нет точки вне круга и секущей; но учащиеся создают ее. Соединив точку А и В продолжив этот отрезок до встречи с прямой KL в некоторой точке С, СА*СВ=СТ2, где Т – точка касания. Из этого уравнения учащиеся находят СТ, Таким образом к двум данным точкам А и В на окружности они присоединяют еще одну найденную точку. Т той же окружности. За тем, зная три точки окружности, чертят ее.

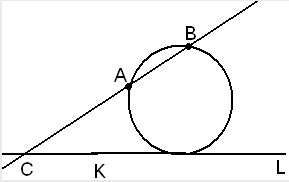
В условии задачи не упоминалась секущей – учащийся должен по своей инициативе ввести ее в чертеж, чтобы найти путь к выполнению требуемого построения. Весьма много инициативы и изобретательности учащийся вынужден проявить при решении трудной геометрической задачи на построение и при отыскании новых способов выполнения требуемого построения.

8. Геометрические задачи на построение приучают учащихся проявлять настойчивость в достижении намеченной цели.

Многочисленные наблюдения показывают, что при умелой постановке преподавания геометрии учащиеся охотно решают не только задачи повышенной трудности, помещенные в учебниках и задачниках, но и те задачи этого рода, которые встречаются в других учебных пособиях, причем при отыскании требуемого построения не останавливаются перед затратой значительного количества времени и труда.

9. Геометрические задачи на построение приучают учащихся логически рассуждать.

Действительно, в чем состоит процесс решения каждой геометрической задачи на построение? Учащиеся ставят перед собой определенную цель: выполнить требуемое в задаче построение. Для достижения этой цели ему приходится, прежде всего, хорошо вдуматься в содержание условия задачи, припомнить необходимые сведения из геометрии. Только в самых простых геометрических задачах на построение оказывается возможным сразу же выполнить требуемое построение. В большинстве случаев прежде чем получить возможность осуществить искомое построение, необходимо предварительно сделать одно или несколько вспомогательных построений, каждое из которых представляет результат логических умозаключений. Первое вспомогательное построение целиком основывается на данных условиях задачи и на определенных геометрических сведениях, без знания которых невозможно решить рассматриваемую задачу. Если появиться необходимость во втором вспомогательном построении, то первое вспомогательное построение включается в число данных. Выполняя одно за другим вспомогательные построения, учащиеся, наконец, приходят к возможности выполнить искомое построение. Вспомогательные построения вообще являются целесообразно направленными попытками, но всегда каждое из них приводит к желаемой цели. Поэтому в процессе решения геометрических задач на построение приходится отбрасывать те вспомогательные построения, которые не упрощают ход решения, а усложняют его или даже приводят в тупик. Таким образом из всех логически возможных построений приходится выбирать наиболее подходящие, наиболее быстро приводящие к цели. Найдя способ выполнения требуемое построение, учащийся должен, во-первых, логически обосновать правильность каждой из отдельных операций этого построения, и во-вторых логическими рассуждениями установить, всегда ли рассматриваемая задача имеет решение и сколько оно допускает решений в отдельных случаях.

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике